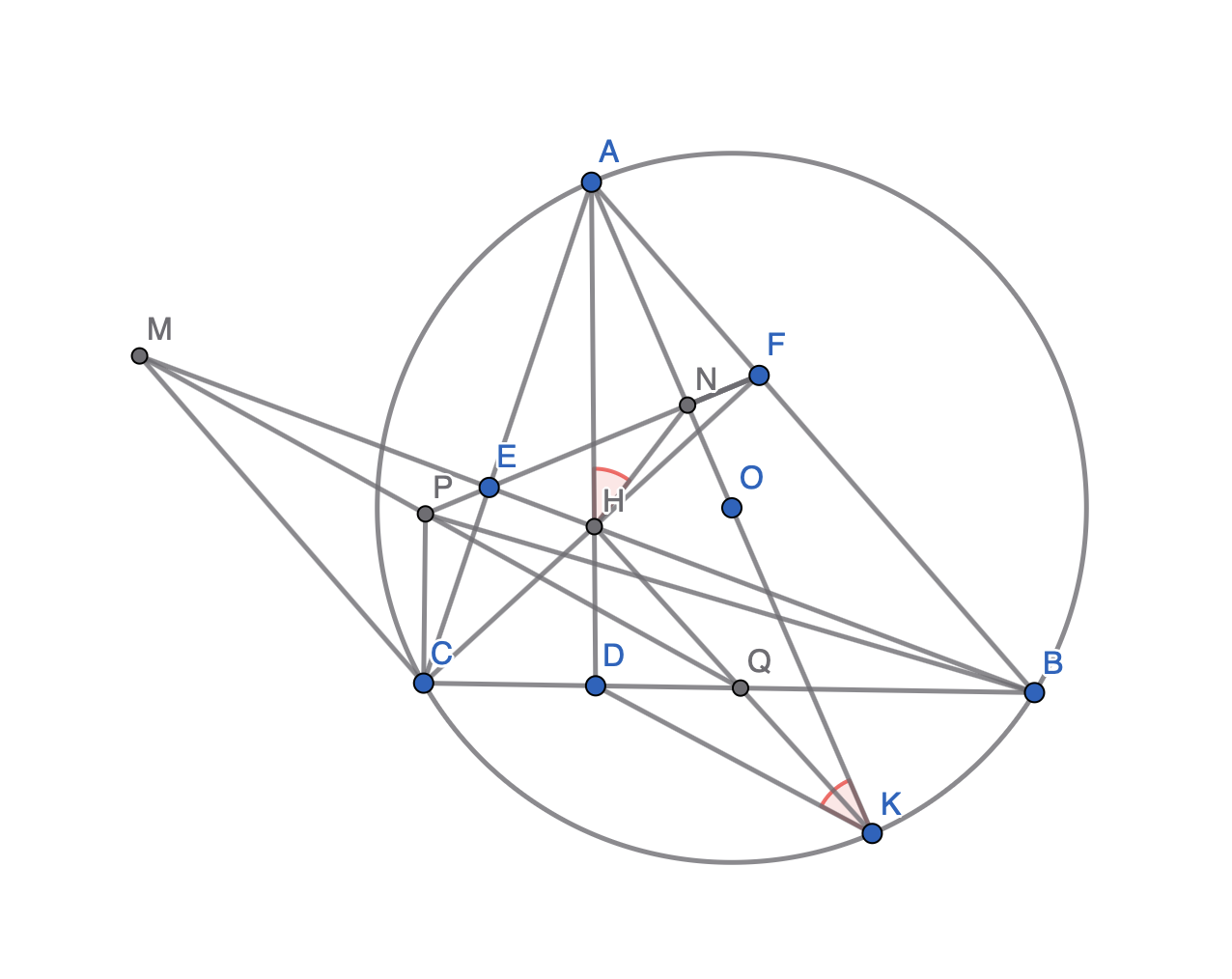
Nghe An - Problem IV - 2025-26

Let $\triangle ABC$ be an acute triangle $(AB > AC)$ inscribed in the circle $(O)$ with center $O$ and radius $R$. The altitudes $AD$, $BE$, $CF$ intersect at $H$. Let $AK$ be a diameter of $(O)$, and let $AK$ intersect $EF$ at $N$.

(a) Prove that $BKNF$ is cyclic and that

$$\angle AKD = \angle AHN.$$

(b) The line through $C$ parallel to $AB$ meets $BE$ at $M$. Let $Q = BC \cap HK$, and let $P = EF \cap QM$. Prove that $\triangle BPC$ is right-angled.

(c) Assume $A$, $C$, and the circle $(O)$ are fixed, with $AC < R\sqrt{3}$. Point $B$ moves on the major arc $AC$. Find the position of $B$ that maximizes the sum of perimeters of $\triangle AEF$, $\triangle BFD$, and $\triangle CED$.